Class-prior estimation in a semi-supervised setup

Problem formulation

In this problem, we have a fully labeled training dataset:

$\displaystyle \left\{ x_i, y_i\right\}_{i=1}^{n_{tr}} \sim p_{tr}(x, y),$

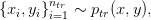
and an unlabeled dataset drawn according to:

$\displaystyle \left\{ x_j'\right\}_{i=1}^{n_{te}} \sim p_{te}(x).$

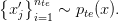
We assume that the test and training datasets only differ by a change in class priors:

$\displaystyle p_{tr}(x|y) = p_{te}(x|y), \quad p_{tr}(y) \neq p_{te}(y).$

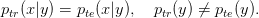
The goal is then to get an estimate 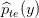$\widehat{p}_{te}(y)$ , that would allow us to reweight any empirical average
calculated using the training samples:

$\displaystyle \int{\ell(yg(x))p_{te} dx} \approx \sum_{y=1}^c \frac{1}{n_y}\sum_{i=1, y_i = y}^{n}\ell (y_ig(x_i))\widehat{p}_{te}(y).$

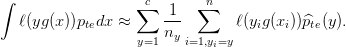
The general strategy that we follow is to have the following model of the test input density:

$\displaystyle q(x; \theta) = \sum_{y=1}^c \theta_y p_{tr}(x|y).$

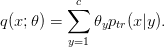
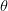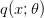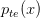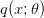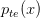We then select $\theta$ so that the model $q(x; \theta)$ is the same as $p_{te}(x)$ . To compare $q(x;\theta)$ and $p_{te}(x)$ , we
use a divergence (such as an 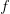$f$ -divergence or 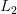$L_2$ -distance). These can in turn be directly estimated from samples (avoiding density estimation).

We provide implementations for two methods:

Note that experimentally, the 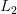$L_2$ -method seems to give the best results.