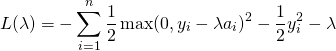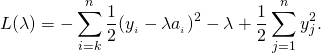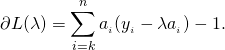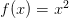Conjugate of piecewise function
In this post, we’ll show how to calculate the conjugate of a piecewise function ![]() ,
,
such as
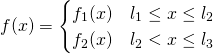
The conjugate for the above is:
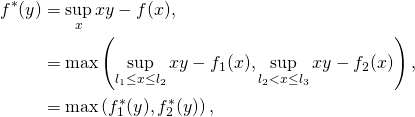
where ![]() is the conjugate of the function
is the conjugate of the function ![]() constrained to
constrained to ![]() . So, computing the conjugate of a piecewise function is simple as long as the conjugates of the sub-functions can be computed easily.
. So, computing the conjugate of a piecewise function is simple as long as the conjugates of the sub-functions can be computed easily.
Conjugate of constrained function
In this section, we’ll show how to calculate the convex conjugate of a function ![]() , which is the function
, which is the function ![]() which is constrained to a domain
which is constrained to a domain ![]() .
.
The conjugate is defined as:
![]()
For the unconstrained case, the solution would be given by:
![]()
where ![]() is the derivative of
is the derivative of ![]() . Since
. Since ![]() is convex,
is convex, ![]() is a monotonically increasing function. Therefore, we have
is a monotonically increasing function. Therefore, we have
![]()
The conjugate of the constrained function is therefore:
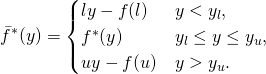
The convex conjugate for the unconstrained function can be automatically calculated in Python — as described in the previous post.
Code that do the above is given below:
def calc_const_conj(fun_str, lstr='l', ustr='u', varnames='x l u', fname='plot.png'):
# set the symbols
vars = sp.symbols(varnames)
x = vars[0] if isinstance(vars, tuple) else vars
y = sp.symbols('y', real=True)
# set the function and objective
fun = parse_expr(fun_str)
obj = x*y - fun
fun_diff = sp.diff(fun, x)
obj_diff = sp.diff(obj, x)
l = parse_expr(lstr)
u = parse_expr(ustr)
# calculate yl and yu
yl = sp.simplify(fun.subs(x, l))
yu = sp.simplify(fun.subs(x, u))
dyl = sp.simplify(fun_diff.subs(x, l))
dyu = sp.simplify(fun_diff.subs(x, u))
# calculate derivative of obj and solve for zero
sol = solve(obj_diff, x)
# substitute solution into objective
solfun = sp.collect(sp.simplify(obj.subs(x, sol[0])), x)
# print the function and conjugate:
print('{0:45} y < {1}'.format(str(sp.simplify(l*y - yl)), dyl))
print('{0:45} {1} <= y <= {2}'.format(str(solfun), dyl, dyu))
print('{0:45} y > {1}'.format(str(sp.simplify(u*y - yu)), dyu))
# Example: calc_const_conj('1/2*x**2', lstr='-1', ustr='1', varnames='x')
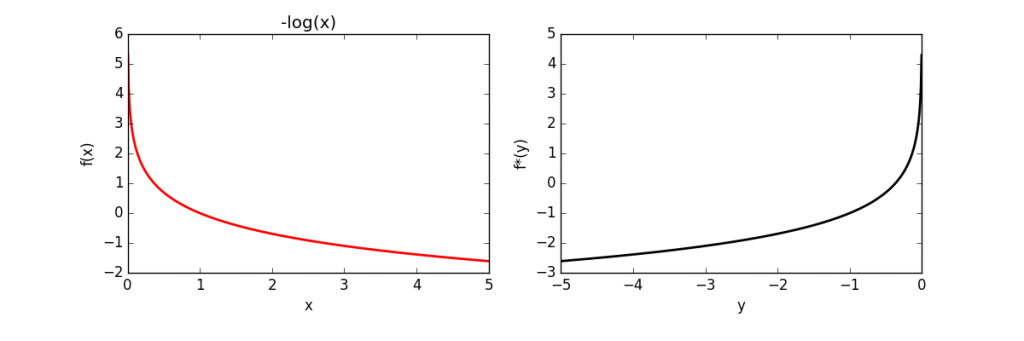
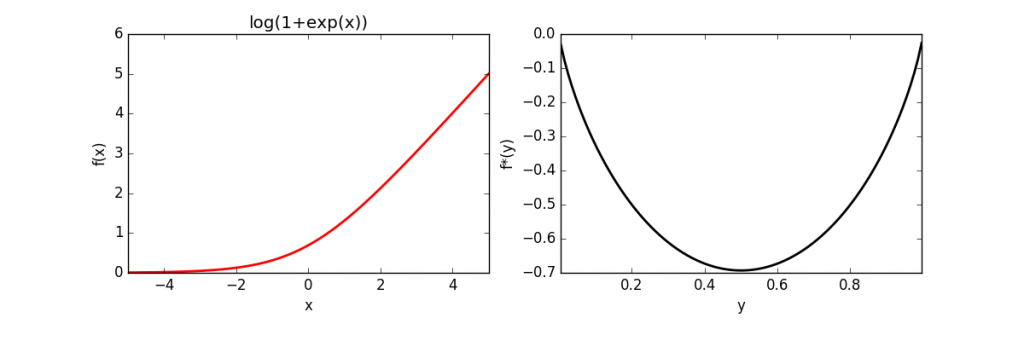
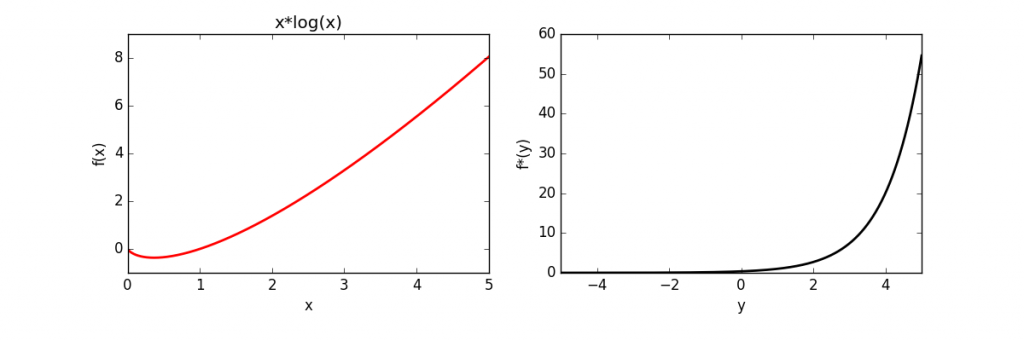
Table of conjugates
| Function | Constraint | Conjugate | ||
| Linear | 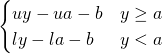 |
|||
| Simple Quadratic | 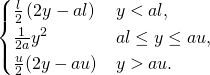 |
|||
| Quadratic | |
|
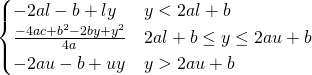 |
|
| PE-like | |
|
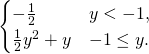
|
|
| Hinge | |
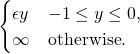 |
||
| (scaled)Hinge | |
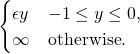 |
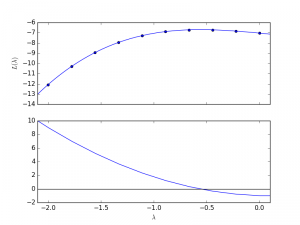
![Rendered by QuickLaTeX.com \begin{align*} L(\lambda) & = \min_{x} \sum_{i=1}^{n}\left[\frac{1}{2}(x_i - y_i)^2 + \lambda a_i x_i \right] -\lambda\qquad \textrm{s.t.} \quad x \succeq 0, \\ & =\min_{x} \sum_{i=1}^{n}\left[\frac{1}{2}x_i^2 - x_i[y_i - \lambda a_i]- \frac{1}{2}y_i^2\right] - \lambda \qquad \textrm{s.t.} \quad x \succeq 0. \end{align*}](http://www.mcduplessis.com/wp-content/ql-cache/quicklatex.com-ec69243cdbdcd49401aaa472a9e2eaa1_l3.png)