Automatically calculating the convex conjugate (Fenchel dual) using Python/Sympy

The convex conjugate (or Fenchel dual) for a single variable function $f(x)$ is defined as:

$\begin{align*} f^\ast(y) = \sup_{x} xy - f(x). \end{align*}$

We assume that $f(x)$ is convex, differentiable and simple (closed-form solution exist for minimum). The conjugate can then symbolically be calculated using the following Python code:

def calc_conjugate(str, varnames='x'):

    # set the symbols
    vars = sp.symbols(varnames)
    x = vars[0] if isinstance(vars, tuple) else vars
    y = sp.symbols('y', real=True)

    # set the function and objective
    fun = parse_expr(str)
    obj = x*y - fun

    # calculate derivative of obj and solve for zero
    sol = solve(sp.diff(obj, x), x)

    # substitute solution into objective
    solfun = sp.simplify(obj.subs(x, sol[0]))

    # if extra values were passed add to lambda function
    varnames = [y] + list(vars[1:]) if isinstance(vars, tuple) else y

    return (sp.sstr(solfun), lambdify(vars, fun, 'numpy'), lambdify(varnames, solfun, 'numpy'))

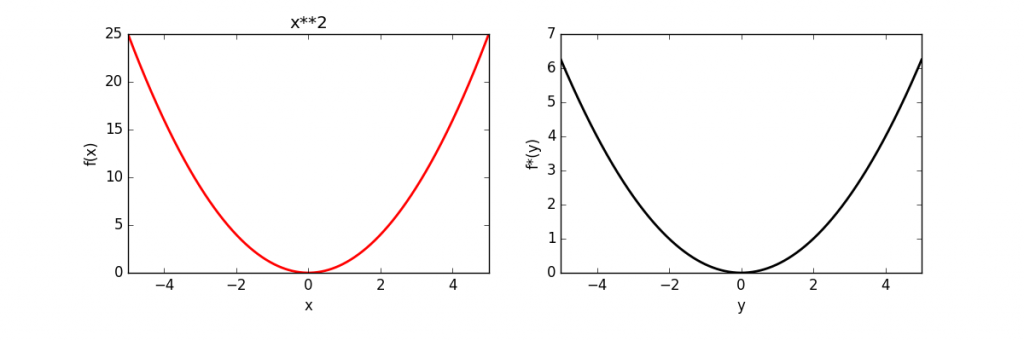
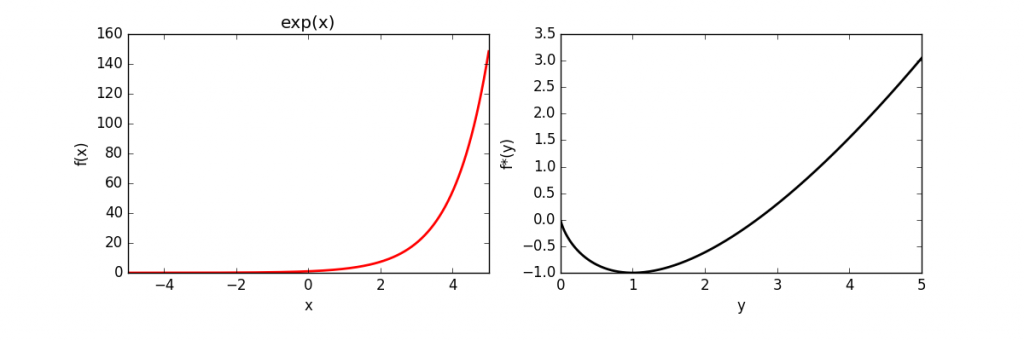
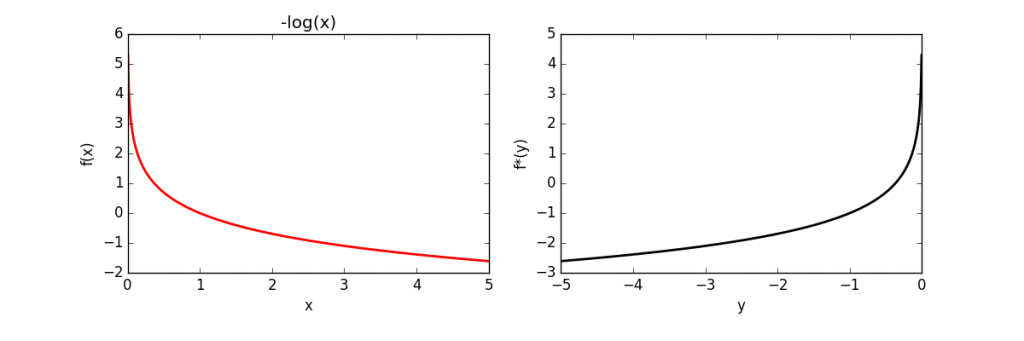
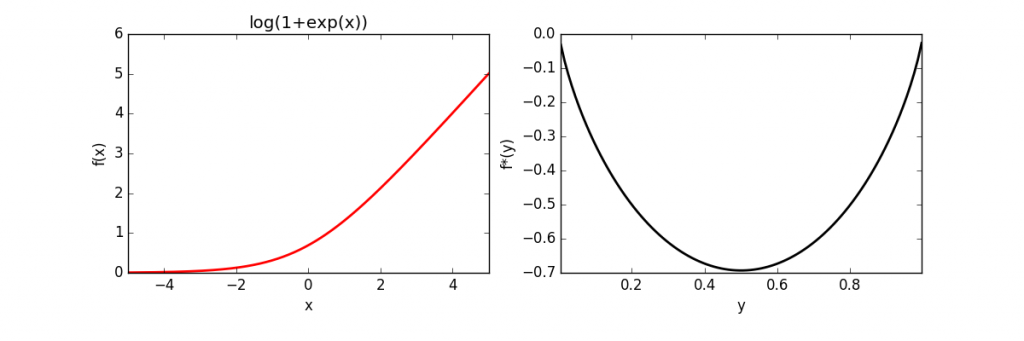
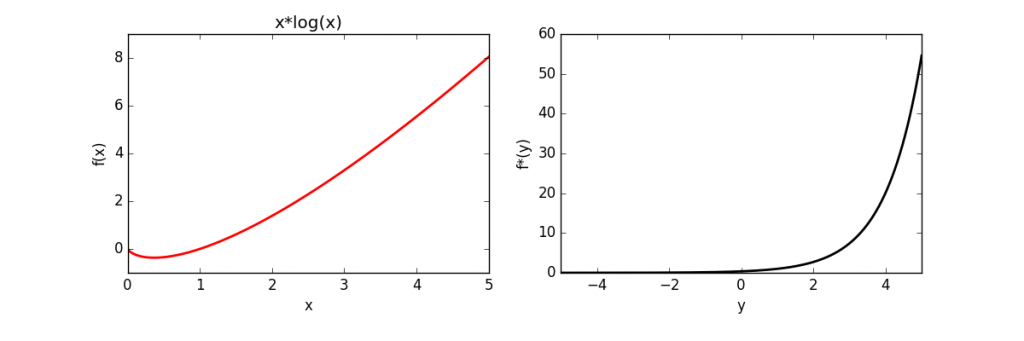
The full source code is here. The above code was used to calculate and plot the conjugates of several functions, which is given below.

	Function	Conjugate
Quadratic	$x^2$	$\frac{1}{4}y^2$
Exponential	$\exp(x)$	$y(\log(y) - 1)$
Log	$-\log(x)$	$-\log(-y) - 1$
Log-Exponential	$\log(1+\exp(x))$	$[1-y]\log(1-y) + y\log y$
x log(x)	$x\log(x)$	$\exp(y - 1)$

Automatically calculating the convex conjugate (Fenchel dual) using Python/Sympy

You may also like

Fast projection onto a Simplex (Python)

Calculation of the conjugate of piecewise functions