Fast projection onto a Simplex (Python)

(work in progress)

Many convex optimization problems can be solved, fairly simply, if the projection onto the constraints can be quickly and simply calculated. By projection onto the constraints $\mathcal{C}$ , we mean the solution to the following optimization problem:

(1) $\begin{align*} \begin{array}{lll} P_\mathcal{C}(y) = & \displaystyle \arg \min_{x} & \frac{1}{2}\left\|x-y \right\|^2, \\ & \textrm{s.t.} & x \in \mathcal{C}. \end{array} \end{align*}$

As an example, the subgradient descent method can incorporate the projection operator to deal with constraints. Here we focus on projection on a simplex: $x^\top a = 1, x >= 0$ . The objective function that we wish to solve is:

(2) $\begin{align*} \begin{array}{lll} P_\mathcal{C}(y) = & \displaystyle \arg \min_{x} & \frac{1}{2}\left\|x-y \right\|^2, \\ & \textrm{s.t.} & x \succeq 0, \\ & & a^\top x = 1. \end{array} \end{align*}$

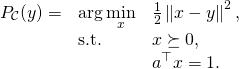
As a test case, we can implement the projection in cvxpy:

import cvxpy as cvx
import numpy as np

def proj_simplex_cvxpy(a, y):
    '''
    Returns the point in the simplex a^Tx = 1, x&amp;amp;amp;amp;gt;=0 that is
     closest to y (according to Euclidian distance)
    '''
    d = len(a)

    # setup the objective and constraints and solve the problem
    x = cvx.Variable(d)
    obj = cvx.Minimize(cvx.sum_squares(x - y))
    constr = [x &gt;= 0, a*x == 1]
    prob = cvx.Problem(obj, constr)
    prob.solve()

    return np.array(x.value).squeeze()

We can write the dual as:

$\begin{align*} L(\lambda) & = \min_{x} \sum_{i=1}^{n}\left[\frac{1}{2}(x_i - y_i)^2 + \lambda a_i x_i \right] -\lambda\qquad \textrm{s.t.} \quad x \succeq 0, \\ & =\min_{x} \sum_{i=1}^{n}\left[\frac{1}{2}x_i^2 - x_i[y_i - \lambda a_i]- \frac{1}{2}y_i^2\right] - \lambda \qquad \textrm{s.t.} \quad x \succeq 0. \end{align*}$

Since the $x_i$ decouples (for fixed $\lambda$ ) it can be solved as:

$\begin{align*} x_i = \max\left(0, y_i-\lambda a_i \right). \end{align*}$

The dual objective (which is to be maximized) is therefore:

$\begin{align*} L(\lambda) & = -\sum_{i=1}^n \frac{1}{2}\max(0, y_i - \lambda a_i)^2 - \frac{1}{2}y_i^2 - \lambda \end{align*}$

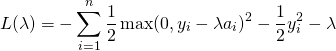
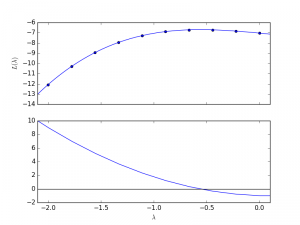
An example of the dual function is given below (source code is here):

As $\lambda$ is decreased from a large value, the values of $x_i$ will “switch on” from $0$ . To determine where the variables will switch on we sort the values according to $y_i/a_i$ .
Consider that we have an index $\mathcal{I}$ that sorts according to $y_i/a_i$ . In other words:

$\begin{align*} y_{I_1}/a_{I_1} \leq y_{I_2}/a_{I_2} \leq \ldots \leq y_{I_n}/a_{I_n}. \end{align*}$

We can refer to these as our indexed $\lambda$ values,

$\begin{align*} \lambda_i = \frac{y_{\cI_i}}{a_{\cI_i}}. \end{align*}$

Suppose that we have a $\lambda$ value. We then want to find an index $k$ , so that

$\begin{align*} \lambda_{k-1} < \lambda \leq \lambda_k. \end{align*}$

We can then write the objective function as:

$\begin{align*} L(\lambda) & = -\sum_{i=k}^{n} \frac{1}{2}(y_{\cI_i} - \lambda a_{\cI_i})^2 - \lambda + \frac{1}{2}\sum_{j=1}^n y_j^2. \end{align*}$

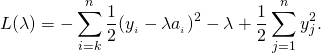
The derivative of the above is therefore:

$\begin{align*} \partial L(\lambda) & = \sum_{i=k}^n a_{\cI_i}(y_{\cI_i} - \lambda a_{\cI_i}) - 1.\\ \end{align*}$

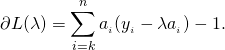
By searching on the sorted list, we get an index $k$ , such that $\partial L(\lambda_k) \leq 0$ , but $\partial L(\lambda_{k-1}) > 0$ .
The optimal lambda value can then be calculated as:

$\begin{align*} \lambda = \frac{\sum_{i=k}^n a_{\cI_i}y_{\cI_i} + 1}{\sum_{i=k}^n a_{\cI_i}}. \end{align*}$

The final algorithm is:

def proj(a, y):

    l = y/a
    idx = np.argsort(l)
    d = len(l)

    evalpL = lambda k: np.sum(a[idx[k:]]*(y[idx[k:]] - l[idx[k]]*a[idx[k:]]) ) -1


    def bisectsearch():
        idxL, idxH = 0, d-1
        L = evalpL(idxL)
        H = evalpL(idxH)

        if L<0:
            return idxL

        while (idxH-idxL)>1:
            iMid = int((idxL+idxH)/2)
            M = evalpL(iMid)

            if M>0:
                idxL, L = iMid, M
            else:
                idxH, H = iMid, M

        return idxH

    k = bisectsearch()
    lam = (np.sum(a[idx[k:]]*y[idx[k:]])-1)/np.sum(a[idx[k:]])

    x = np.maximum(0, y-lam*a)

    return x

Other resources:

MATLAB implementation of projection onto unit simplex (description here)
Michelot, C. (1986). A finite algorithm for finding the projection of a point onto the canonical simplex of∝ n. Journal of Optimization Theory and Applications, 50(1), 195-200.

Todo:

Implement the code in C/C++
Give a better test case
Simplify the explanation and implementation
Give a practical example (e.g. estimation problem with subgradient descent)